The Engineering Team

Posted by & filed under Articles.

It’s all been said before, but here is my version. A number of my statements will be massively generalised but they are made to trigger further debate and discussion.
Numerous reports over many decades have focused on the ineffective state of education and training and our track-record in this area compared with our competitors. The majority of these reports focused on particular sectors of education and training e.g. secondary, further and higher education. Very few, as the main history of technical education showed, embraced the whole of the education and training spectrum. It is important on the grounds of continuity and progression that all stages are considered as part of a continuum. Too often a particular priority is given to one stage of education without careful thought of its consequences on the other stages. Lifelong learning in order to be successful must provide continuity and ease of progression for all people at whatever stage they are. Very often some of the excellent findings and recommendation of these reports were seldom recognised or implemented and the reports gathered dust on the shelves.
What this country has consistently failed to achieve since the Great Exhibition (1851) is to produce a range of suitably qualified people in sufficient numbers to work in teams with the productive and original thinking individuals and researchers. The roots of the problem may be cultural. The culture, in England particularly, is a basic hostility to science and technology and we imagine that success in life as measured by employment in other professions such as financial services, law and medicine. With respect to the people in these professions they do not actually contribute much to the manufacturing base of this country. Wealth generated by such can never fully compensate for a strong and efficient manufacturing base. Just look at the current problems caused by the recession and the highly questionable practices operated by the financial services particularly in the US and UK. (The financial services could be perceived as witchcraft and financial terrorism conducted in pin stripes!) To add insult to injury it is just these services that make money during recessions and depressions. Armies of accountants, auditors, consultants and lawyers make substantial profits from companies going into liquidation as the manufacturing base of this country further crumbles.
The educational system also contributes to this barren perception of science and technology. The system seems to equate quality with rarity and, as has been said before, the educational system is a catalogue of acculative failure. Any educational and training system must surely equate quality with fitness of purpose for all. Most people, given the right set of opportunities, can benefit from programmes of education and training at all stages of their life and then can play a more meaningful part in society and employment.
The ever- accelerating knowledge and skill base currently makes the situation even worse. It is now reckoned that the knowledge half life of an electrical engineer is less than four years and in some areas of IT less than six months. This means that there is a desperate need for lifelong learning and continuous professional development (CPD) for people in work. Successive governments have set targets for education and training attainment but enviably these have failed to be realised.
The country must break with the low- skill equilibrium and adopt once for all a high-skill, high-quality philosophy in the workplace. The current recession coupled with the severe austerity regimes being introduced by the consolation government in the UK will, I fear, perpetuate the low- skill and low-quality economy and employment profile.
In order to break away from its woefully inadequate track record, Britain needs to invest in people, both in the initial stage of education and training, but equally important, make a growing commitment to retraining, updating and up skilling already in work. People are the most valuable resource and it is important that a long-term view is taken of education and training, supporting people to cope with the information technology revolutions that are occurring. As has been said ‘it is not the robots which are the wonderful achievement, but the new and wide-ranging competence of our employees.’ Although many companies in the UK are striving to compete in the global economy the continuing skills gaps and shortages make it difficult for them to match the levels of productivity and work based qualifications of our main competitors. This fact is created by the inadequate state of technical education and training at all levels.
Engineering and Manufacturing
I would like now to focus on engineering and manufacturing, although many of the arguments bear similarities with other key subject areas e.g. the physical sciences and mathematics. Because this country still operates a largely elitist education system, much of the attention is still given to the production of graduates and those people who wish to progress on to chartered engineer status. What we have neglected is the training of technicians, operatives and craftspeople to support engineers, scientists and designers. This deficiency has been around since the Great Exhibition. For every researcher there needs to be four/five support staff, highly qualified and motivated. The area of technician and craft educational training has been woefully inadequate. Again, this might be associated with some cultural factor, that people often see these occupations/jobs as second rate.
Colleges, as the history of technical education shows, play a major role in improving the stock and flow of suitably qualified technicians and craft people. They have never been given adequate resources to achieve the required results within an operational framework based on a long-term strategy. Successive recessions have witnessed dramatic cut-backs in training. The same thing is happening in the current recession where college’s budgets are being cut up to 25%. This is opposite to what happens in many other countries where they increase investment in training/retraining. This country never seems to learn from the lessons of history. If we come out of the current recession we will still be confronted with massive skills gaps and shortages in key areas. The 1980s witnessed a massive decline in traditional manufacturing industries, and it must be said that there were examples of low productivity, over-staffing and under investment in equipment, infrastructure, capital and modern management techniques. This destruction has now reached the critical threshold that we now manufacture very little and have outsourced many of our remaining industries abroad.  The country needs an efficient and viable manufacturing base in order to promote wealth. Increased global competition makes it even more essential. The prevailing view in the current recession is that the economy can be rebalanced by moving ex-public service employees and what remains of the traditional manufacturing industries into new technologies and high value occupations sadly this will not happen without major investments in retraining and up skilling. We must be able to produce products and services that the rest of the world wants to purchase. There needs to be a sensible balance between the manufacturing and service based industries and they must complement each other. The two go together and one cannot have an undue emphasis over the other – at present Britain has got the balance wrong! If we are to develop a regenerated and rebalanced manufacturing base we need to address some very fundamental issues associated with education and training.
When looks at the way companies are evolving internationally, many are down-sizing and becoming flatter and developing total quality management systems around small teams of highly qualified people. Each person within the team has a particular role and sense of the others knowledge and skill. The analogy is often used of ‘the surgeon team’ a small group of highly qualified people who can design products and services and solve problems. In addition a high level of automation must critically match the skills of the team members. There should no longer be issues of demarcation and over-staffing. There is a synergy between team members and also the teams that constitute the organisation. This culture could overcome the ongoing difficulty of attracting women into certain occupations, particularly engineering, as women are proven team workers.
The Engineering Team
This brings me to the concept of the engineering teams, to date; most emphasis has been placed on the graduate and chartered engineer. The engineering team comprises multi-skilled craftspeople, technicians, incorporated engineers and chartered engineers. In order to maximise the effectiveness and efficiency of the team, the education and training of all the members is important. Colleges must continue to develop innovative partnerships with employers and maximise wherever possible work based training through work experience, work placements etc. Colleges must also continue to establish new delivery and study methods that are more acceptable, both in terms of convenience and cost effectiveness to both parties. Apprenticeships must be further extended and their quality improved. In order to produce a more versatile engineer the E model of education and training should be adopted. The E model represents an ongoing and sensible mix of breath, balance and depth (specialisation) in the curriculum experience as opposed to the existing T model with too much early depth (specialisation). Students need to appreciate and experience first-hand the realities of engineering and manufacturing right from the beginning of their studies. This clearly requires stronger ongoing links between college study and the workplace – this reinforces the need and importance for work placement/shadowing/experience and the more formal apprenticeship programmes which are mainly work based. Opportunities for progression of the members of the engineering team must also be facilitated by the curriculum frameworks. The current qualifications framework still presents barriers to progression. The various qualifications, in spite of successive reforms, still cause difficulties for smooth progression. Greater recognition of team members experience and particular skills needs to be given by way of more enlightened use of assessment of prior achievement and learning, professional dairies and portfolios. People with CGLI qualifications still find it difficult to progress easily onto engineering technician, incorporate engineer or chartered engineering status. Similar difficulties still exist for other members wishing to progress to the next stage. The current education and training reforms will hopefully begin to resolve these long standing problems with progression and transfer. When one looks at the current qualifications and possible career routes for engineers it is reminiscent of the vessels on a gnat’s leg. It looks complex and confusing and in many cases does not offer smooth progression. One of the problems causing this confusion is still the multitude of professional bodies that represent engineering and manufacturing and the various members of the team. These bodies still seem to desire to maintain a great degree of autonomy and as a result are very protective of their territorial domains. As the world of work moves to multi-skilling and cross-skilling, it is surely important that a number of these associations and professional bodies merge and create a more unified structure to represent and support engineering and manufacturing. These professional have a long and creditable history (see biographies and pen portraits) but the time is right to reform and rationalise in order to improve the image of the disciplines. In order to create the engineering team all the interested parties must work together to eliminate unnecessary barriers that will establish an educational and training system that recognises the value of each team member and promotes a positive image of engineering and manufacturing. Once a highly qualified and motivated culture is created perhaps the country can re-establish and rebalance its economy. The country has relied on financial services, real estate and property and a disproportionately sized public services for too long and that imbalance has now to be addressed and resolved. 

The Darwinian Paradox?

Posted by & filed under Articles.

 
A different and somewhat divergent take on college management?
One of the more acceptable and helpful tenets of effective and good management and leadership is that managers should adopt a reflective and more critical stance. Continuous, systematic and careful reviews of the processes and outcomes of the business are, indeed, an invaluable and essential aid to the effective manager and leader.
Technical colleges as all educational and training institutions have much to reflect in the current climate of budget cuts and unprecedented austerity and hastily introduced government reforms to the curriculum, institutional governance and inspection regimes. The parenthesis model of management has never been more valid. The model challenges the whole of the existing thinking on organisational theory. It identifies a new type of person, namely the parenthetical person, one who reflects and reacts to the new societal circumstances facing the world. Simple definitions of inputs and outputs, as currently defined, are naive and simplistic.  A Chinese proverb brilliantly reflects the need to be flexible, responsive and pragmatic namely: ‘cross rivers touch stones.’
The approach states forcefully that it is not enough merely to manage an organisation but it is necessary to attempt to manage the whole environment in which the college exists. It is essential that all managers and leaders perceive the broader societal implications of their managerial and leadership functions. Colleges are currently exposed to a very volatile environment. The education and training landscape in which they operate comprises a series of fragmented elements including funding agencies, many of which introduce policies and strategies that are contradictory and paradoxical. These impact on the institutions and require totally new forms of management and leadership skills. The continued development of market-force philosophies makes it difficult to seek sanctuary in the past. Even the awarding bodies are now operating and defining education and training in terms of hard headed businesses. As a result it often strikes me as being a classical example of Darwinism.
Historical practices and sign posts are often of little help. This is in itself is no bad thing. Many practices in education and training are still plagued by atavism so one must be prepared to accept change, development and improvement as inevitable. One, however must ask whether all changes are necessarily good for the educational/training service and are some of the changes precipitated by questionable external imperatives just bring change for changes sake e.g. examples of political short termism or political dogma?
Natural Selection
So, during a period of reflection I explored the possible links between Darwin’s theory and current education management. Evolution theory is about progression and the imperative of the survival of the fittest and strongest. This looks a promising connection, especially in the current (free?) market forces where competition and (quasi) institutional autonomy is encouraged. Recruit more students with fewer resources, which clearly means ‘do more for less’ threaten some strategically important provision in such areas as construction, engineering and the physical sciences. Sadly these subjects along with others like mathematics and statistics continue to struggle to recruit sufficient students. One just has to read comments from employers about the lack of sufficient and properly qualified graduates in these subjects and other vocational areas of study. The often simplistic accountancy driven methodologies make it increasingly difficult for managers to protect high-cost, low recruiting programmes of studies. The funding regimes that are introduced quite rightly require gains in efficiency and effectiveness and the elimination of anarchic practices, but the regimes are not able to fully recognise certain vulnerable areas of study i.e. they lack sensitivity. It would therefore seem that we do manage a Darwinian scene and that managers must make every effort to protect threatened strategic programmes.
Constant Improvement
Just as Darwinism is about progression and advancement, in the natural world, education must be about constant improvement of the service offered to all its students whether in employment, entering employment or as citizens in general. Provision must be of the highest quality as possible and match the future requirements of life and work. The early theories/hypotheses of evolution were about long-term change and improvement: this was called ‘phylogenic gradualism’. Species coped successfully or otherwise with a whole range of external forces and adapted to these influences. It was usually about long-term developments, progression, survival and ultimately improvement.
In the light of more recent observations, data and field research a refined hypothesis has been postulated, namely ‘punctuated equilibrium.’ Distinct and discernible changes are observed, often over short time scales.
So which of these hypotheses is more valid in the current climate? Changes come thick and fast and often precipitate rapid and unforeseen mutations/consequences, so it would seem that punctuated equilibrium – or should that be ‘rapid punctuated equilibrium’? is more appropriate to the world of education and training. Where the analogy with Darwinism breaks down, or weakens, is that much of the current change in education/training is regressive, not progressive. Mass scale introduction of accountability structures and bureaucracy, much of which seeks information to a ridiculous and questionable degree of resolution diverts the colleges from their true business, namely improving access and participation of students, increasing the effectiveness of learning and teaching and increasing achievement levels. This diversion seriously affects the quality of service as the learner-staff have to respond to innumerable requests for information and become more involved in administrative tasks. Also the obsession with testing and increasingly heavily prescribed syllabuses further constraint teachers and learners even more. Leagues tables and questionable targets abound linked with obsessive and intrusive inspection and assessment regimes.  Perhaps a modified version of rapid punctuated equilibrium indicating regression is a stronger case to consider?
Different sponsors/organisations require different forms of information at different times, although in many cases they are asking for the same measures. No apparent coherent or long –term strategic planning process exists between these sponsors/organisations, especially in the area of education and training. To extend the Darwinian hypothesis perhaps one could identify these sponsors/organisations as forms of predators-maybe-but that is worth a longer and separate period of reflection.
So there are a number of parallels, some strong, some weak, between education and Darwinism. The external environment can be both supportive and hostile and managers and leaders must deal with a multitude of external influences operating on short-term political agendas and policies, often in contradictory fashions.
Policy, planning and strategy determined by humans are too often driven by a range of many interconnected values e.g. political and ideological which are placed on human worth. The parenthetical manager and leader, referred to earlier, will also assert some values for the organisation and the external environment which means that the manager and leader must be aware of these values and as a result cope more effectively with change-or should it be rapid punctuated equilibrium?   
References:
Bush. T. ‘Theories of Educational Management.’ Paul Chapman. 1988.
Bush. T. (ed). ‘Managing Education Theory and Practice.’ Open University. 1989.
First published in ‘t’ magazine.

The Importance of Workplaced Mathematics – Can the problems be resolved?

Posted by & filed under Articles.

 
Questions continue to be raised about the teaching and learning of mathematics in schools and colleges and the relative levels of participation in the subject post-16. Questions continue to arise about its purpose and centrality in the schools national curriculum and the introduction of functional mathematics in vocational awards. In addition, concerns are being raised about the quality and quantity of students entering further and higher education to study courses that require mathematics.
We live in a technologogical society based on mathematics and science, so it is perplexing that schools, colleges and universities continue to turn out students in large numbers who not only lack adequate mathematical and numeracy skills but also the students constantly state that the subjects are boring and irrelevant. There surely needs to be a vigorous national debate, on ways to tackle this complex and multidimensional problem.
Hopefully these debates will once and for all establish a consensus about these problems with the subjects and how to resolve them. Equally importantly is the urgent need to recognise and identify the problems associated with these subjects in the workplace. Work-based mathematics and numeracy are too often overlooked and neglected when reviews are carried out. Meaningful research on mathematics and numeracy in the work place has been minimal and as a result there is a dearth of evidence and even then scant attention paid to what the real issues are.
Towards a new lexicology
This situation is partly explained by the fact that clear understandings of the factors and determinants involved in work based mathematics and numeracy have not been established. It is also essential to develop more precise definitions of the various elements involved. In any research there is a requirement that a precise lexicology is developed and adhered to. These requirements are important given the different mathematical and numerical skills and competences that exist in different work place situations e.g. health professions, process plant operations, retailing/distribution, construction crafts etc. Key questions need to be answered including:
·         What mathematical and numerical skills are important in each identified work situation and how best are these identified?
·         What attitudes towards numeracy and mathematics need to be developed and encouraged by employers, employees, parents and teachers?
·         How best can these subjects be taught and learnt in traditional classroom situations and how important is the context in which teaching and learning takes place?
·         How does the context of numeracy and mathematics in the workplace become formalised in order to bring about an identification and understanding of the kind of skills that are needed in a given setting?
In the limited research on numeracy in the workplace, the lack amongst many emplees of ‘a feeling for number’ has been highlighted as a problem. It would seem that the school curriculum particularly at primary level has paid little attention to this extremely important element and it remains to be seen if the numeracy strategy will bring about a sustained and lasting improvement.  The inability to manipulate and understand the fundamental operations associated with number creates later problems irrespective of the ultimate aspiration of the learners. For example, the inability to estimate and transpose numbers and equations makes for fundamental difficulties later.
Too often in the past, reforms to the mathematics curriculum diluted these essential building blocks for numeracy skills. An illustration is given in the classic book by Jan Gullberg (1) in the following quote:
‘In the 1950s educators and reformers introduced the language of sets as a basis for mathematical studies in schools. Many pupils started studying sets before they could count the number of elements in the sets. The language of sets and the surrounding ‘New Maths’ created chaos in schools in the 1950s, 60s and 70s. It was a frustrating time in education. Strange symbols were introduced for seemingly simple things: teachers had to be retrained and most parents had no idea what their children were doing in mathematics.
The concepts of set theory are simple, but they require a precision and maturity of language that is beyond the power of many learners. An idea that was meant to simplify in fact complicated matters. A dull but useful drill was replaced by a dull and useless drill. In England and many countries the New Maths created a generation with sometimes very limited arithmetic skills’
This long but helpful and insightful quotation highlights an important issue in the wider debates on work based mathematics and numeracy namely the essential need to lay the foundations of these important subjects. The relevance and fitness of purpose of the school/college mathematics content needs to match the future needs and aspirations of the learners.
This is important, as the young adults leaving these institutions will enter a wide variety of work situations and occupations that will in turn require varying degrees of numerical and mathematical skills and competences. Careful thought and analysis is needed to identify and then introduce the appropriate content at the right time into the curriculum.
The role of employers.
Clearly there are fundamental elements that all learners require to learn but with the necessary differentiations that reflect their ability and career intentions. It must be accepted that very few will study mathematics to any depth whilst the vast majority will require a basic foundation and grounding in numerical skills and mathematical techniques in order to cope with the needs of chosen occupations. The curriculum needs to be configured to recognise these demands and at the same time excite and stimulate the learners whatever their needs.
One real challenge for the curriculum reformers is the fact that the whole curriculum is by definition restrictive, arising from the necessity of including other key curriculum subjects whether in the core offer of in course options. The expectation that numerical skills and mathematical techniques taught in schools and colleges should be capable of satisfying the total needs of the learners whatever their career intention is absurd. Thecontent must be seen as relevant and be significantly informed by employers. Employers must be involved in assisting the identification of what is required in their particular work place. Sadly to date this essential element has been lacking. The primary challenge is to provide the necessary grounding to the learners both those starting work and equally important for those already in work.
The recent farce surrounding the introduction of functional mathematics again highlights that there is still a long way to go before the problems with the teaching and learning of work based mathematics and numeracy are resolved.
Let us hope there will be along and meaningful debate of this strategically important topic.
(1)   Gullberg J. ‘Mathematics from the Birth of Numbers.’ Norton and Company. 1997.

How Effective are Current Labour Market Techniques?

Posted by & filed under Articles.

The only certainty is uncertainty itself
An important, challenging and yet an intriguing question to ask is: How effective is current labour market research in identifying skills shortages and gaps and the statistical models to use to illustrate the shape and nature of employment profiles in the future? It’s an important question to ask, as it is essential to refine and enhance the statistical techniques that are used today in order to improve the predictions and monitoring of future labour market dynamics. Labour market information and data provides the foundation upon which much of a government’s planning and subsequent expenditure is based and has a significant influence on future policy and predicted expenditure on such critical areas as technical and vocational education and training.
The massive transitions and transformations occurring in the current rapidly changing global labour markets must surely require more sophisticated statistical techniques. The global labour market is becoming even more volatile as technological innovation continues to accelerate. The transitions and transformations in the global economy include:
Ø Demographic trends e.g. the increasing proportion of an aging population of workers in many industrialised nationsbecause of decline in birth rates compared with higher birth rates in many emerging economies
Ø Changing career and work profiles i.e. multiple careers throughout people’s working lives coupled with different modes of working e.g. part-time and home based working
Ø Increased world-wide mobility of the workforce
Ø Impact of changing cycles of out sourcing e.g. companies pursuing cheaper labour markets
Ø Changes in company structures resulting from mergers and acquisitions resulting in more complex human resource legislation and regulation
Ø Increasing influence of multi-national companies and enterprises.
In such a changing and increasingly complex global environment more effective statistical techniques and modelling methods are urgently required. New measurement instruments and databases, which can more effectively match, identify and articulate with this new emerging global trading and economic landscape must be developed. In addition more relevant information involving greater attention to cross-occupational sectors and international data and indicators are essential in order to illuminate and inform business and political policy making. One immediate problem here is that the large multi-national companies will be reluctant to share business sensitive information. Problems caused by the current market research could include:
Ø Inadequate knowledge of what competences, skills and knowledge will be required in the future
Ø The resultant mismatch between the products of education and training and the needs of the employers
Ø The resultant growing complexity and inability to achieve a balance in the supply and demand equation
Ø The inability to monitor and capture the knowledge half life of a number of disciplines e.g. IT
A number of statisticians (1) have argued that the current labour market approaches and subsequent analysis represents a classic case of measurement without knowledge. One such commentator, Garonna, has observed; “Measurement gaps and the lack of quality data are the main obstacles to shedding light on the crucial set of relationships between the acquisition and accumulation of knowledge and labour market performance”. One of the intriguing aspects currently is that we have more data from a wide range of disparate and disconnected sources but this does not necessarily provide more reliable, valid and meaningful information. More accurate and accessible statistics and information are necessary to inform international and national labour market intelligence within the global context.
Bearing in mind some of the earlier disasters in this country when using so- called workforce planning e.g. teachers, doctors and the trades such as plumbing, one wonders why many of the current techniques continue to be used to inform future labour markets. Recent surveys and reports highlighting current and future skills shortages in this country still seem to be using the more traditional statistical techniques. This will I fear have serious consequences for the future ability of the educational and training systems to produce a workforce that will compete in the global economy and match the needs of employers.
(1)   Carlson, B, A. (2001). Education and the labour market. Serie dessarroolo,114 UN
(2) Garonna P et al, (2001). Achieving transparency in skill markets. International Labour Organisation. Milan

Gold Standard?

Posted by & filed under Articles.

‘A’ levels have dominated and largely determined the structure of post-16 curriculum in England, Wales and Northern Ireland for over half a century since their introduction in 1951 when they replaced Higher School Certificates. Since their creation ‘A’ levels have been the predominant system for selecting people for entry to Higher Education (HE) and the traditional English three-year single honours degree programmes. This primary purpose was initially successful bearing in mind the relatively small numbers of grammar and private school students entering the examination. It must be remembered that ‘A’ levels were initially aimed at just 2% of the 16-19 aged population many at grammar and private schools and as such was an elitist examination. It is important to remember that the education system is largely determined and driven by class divisions and snobbery that still persist today. Academic subjects are seen as being more important than technical/commercial/vocational education and training. However as the numbers of candidates increased and the learner populations became more heterogeneous and their subject choices more diverse that logic came into question. Increasingly adult students took the examinations pursuing different modes of attendance and study which also raised questions about its structure, content and assessment methods.
In comparison with other equivalent qualifications ‘A’ levels have survived remarkably well but have attracted some criticism over the years. As a result of these concerns a number of major reviews have been instigated but have brought about little change let alone answered the criticisms.
These criticisms centre on a number of concerns namely:
Ø Depth (specialism) vs balance and breadth
·                  ‘A’ levels are unique in offering specialised qualifications based on single subjects possessing as a result depth but providing little real opportunity to study for balance and breadth. For example students could elect to study subject combinations that involved only the sciences or humanities, or social sciences or the arts. This is acceptable for the more specialised degree programmes but as the candidate numbers increased they increasingly exercised greater choice of subject combinations which has highlighted one of the fundamental weaknesses of the ‘A’ level system. This increasing trend of opting for mixed economy programmes has paradoxically attracted the opposite criticism particularly from employers and a number universities namely that the subject profile lacks any real focus or specialist theme. It is this inability of the ‘A’ level framework to provide a balanced overall outcome that is a major flaw in its single subject and open choice philosophy. Other countries offer students a broad-based education in a main field of study alongside some opportunity to specialise – the International Baccalaureate (IB) being a good example of this approach
Ø The almost complete lack of a vocational focus
·                  The focus on single subjects as mentioned above also neglects emphasis on the application of the acquired knowledge and skills and the prevailing view held by many people was that students would gain that practical knowledge once in employment. A couple of examples of this unfortunate belief was the failure to recognise and accept Design and Technology awards and equally surprisingly the rejection of ‘A’ level Engineering by the Engineering professions and universities. Rejections of this kind reinforced negative attitudes to more vocational ‘A’ level qualifications. It was believed that other qualifications would deal with the practical aspects of learning e.g. CGLI/BTEC awards
Ø The primary purpose of the ‘A’ level qualification for the entry to Higher Education (HE) studies
·                  The mismatch between the overall needs of current learners and this primary purpose is now in question. For many students who do not wish to go on to HE the qualification and associated curriculum is increasingly inappropriate. This fact is unfortunately reinforced by the generally held perception that other equivalent qualifications are second class and students as a result decide to study ‘A’ levels. Unfortunately most parents and teachers seem to believe that ‘A’ levels are the gold standard – the beacons of high standards and reliability. Sadly careers guidance and advice often reflects the teacher’s own limited experience of work outside the education system. After all because of the longevity of the qualifications many people are only aware of the ‘A’ level system. Numerous attempts have been made to develop alternatives, (see later), but none have managed to break the strangle hold of ‘A’ levels. Many of the reviews and subsequent reforms have advocated an intermediate award and more recently vocational alternatives at the same level (see later).
When one analyses how the previous proposed reforms of the system have addressed these concerns one can identify a number of approaches:
Ø Increase number of subjects each with a reduced syllabus content. The Schools Council proposals for N and F level examinations (1973) first advocated this and the Higginson Committee (1988) proposed five leaner ‘A’ levels. Both these reforms were rejected and ‘A’ levels continued to dominate the 16 to 19 curriculum.
Ø Change the assessment system. Assessment was always based on an end of programme unseen examination with no real involvement of teachers. They could opt to be employed as examiners with particular boards and contribute to marking and moderation. Various attempts were made to increase the amount of course work i.e projects, open book examinations which allowed more opportunity to liberate the learning and teaching but again this was a short–lived initiative and only in a few subjects was this more enlightened approach allowed namely Art and Design. Opponents of his argued it reduced standards and a similar fate occurred with modularity and unitisation of the A level curriculum. This group formed a powerful lobby who argued end examinations sustained public confidence and credibility in the ‘A’ levels and maintained independence from schools, colleges and teachers.
Ø Introduction of core (key) skills.
For a number of critics the absence of any real curriculum requirements beyond those assessed in the subjects was a problem particularly in the light of the growing concerns about declining competence in numeracy and literacy. As a result a short–lived development in 1989-90 attempted to introduce these as core skills but this never really succeeded. This approach was resurrected by Dearing review but again had limited success mainly because of the attitudes of many teachers who felt in was demeaning for ‘A’ level students to study such topics even in spite of growing concerns from university entry tutors about the declining levels of mathematical/numerical and communication skills from prospective students. As a result core skills mainly focussed on non-‘A’ level students. Core skills eventually transmogrified into key skills comprising communications, application of number with a third recently added for IT. Key skills are very important and must surely be an integral part all qualifications and that most certainly includes ‘A’ levels. One Tomlinson proposal thankfully accepted by the government was the possible introduction of functional mathematics into the future structure both the then proposed vocational diploma and ‘A’ levels.
Ø New forms of qualification. A number of worthy attempts were made to replace ‘A’ levels over the past couple of decades which if adopted would have brought about a significant improvement to the post-16 curriculum. Space does not allow a complete review of these proposals but three merit a mention and involve the introduction of baccalaureate type frameworks and a general vocational set of awards (GNVQs).                                                                The first proposal was the British Baccalaureate (BB) published by the Institute of Public Policy Studies with which a number of key Labour Party people were associated who later became significant members in the government after 1997 e.g. Tessa Blackstone, David Miliband. This and later proposals advocated a unified framework as opposed to an overarching framework embracing different qualifications. The BB also placed great emphasis on modularity, unitisation of the curriculum and innovative assessment regimes based on “fitness of purpose”. The unified approach would bring together the so-called academic (‘A’ levels) and the vocational qualifications and remove the vocational-academic divide. Interestingly once in power the government totally neglected this radical reform. The BB proposals were followed by the Royal Society’s “Beyond GCSE” which again advocated a unified framework based on the best elements of the International Baccalaureate namely subject domains that would realise all the elements of depth, breadth and balance. The Society as one would expect stressed the essential need to continue science and mathematics beyond 16 alongside the students’ main subject elections. However all these proposals and others that followed were rejected. One of the latest examples is the rejection of the Tomlinson proposals for an overarching diploma and the preservation of ‘A’ levels with a watered down diploma for vocational qualifications. Hence the sanctity of ‘A’ levels is maintained and the academic and vocational divide continues. The continuation of the duel system will perpetuate the view that vocational qualifications are second-class and parity of esteem between the qualifications a distant dream. The final example given here is the introduction of the General National Vocational Qualifications (GNVQs) in 1991 which attempted to bridge the gap between A levels and the work-based route personified by CGLI/BTEC/ other awarding bodies. Launched with great gusto and evaluated to death they failed to attract sufficient students at all the three levels that were offered namely foundation, intermediate and advanced. Many colleges tried to make GNVQs succeed but again history and prejudice intervened, the majority of them continuing to take GCSEs and ‘A’ levels. As someone involved in the Royal Society group and the GNVQ developments I know how carefully colleagues considered the benefits that would follow such reforms by creating a more fairer and just system for all learners irrespective of their career intentions and personal expectations. Again short term political expedients over ruled educational logic and reality.
  As one can see from the above commentary the proposed reforms have been numerous and frequent and yet no real change has occurred. One negative outcome from these reviews and their subsequent rejection is the reinforced belief by the ‘A’ level supporters that the qualification is sound and secure. What changes have occurred are incremental as opposed to radical reform and always sadly driven by political imperatives e.g. the value politicians put on the attitudes of some voters from middle England whom they believe will determine the outcome of general elections. This has been reflected over many years by successive rejections of the numerous groups who have suggested reforms of ‘A’ levels.
Other aspects that are overlooked by the critics and supporters of ‘A’ levels is the distortion and tensions that the ‘A’ level system creates in the education system. ‘A’ levels have always been strongly influenced by the university system. Universities created the majority of examination boards as evidenced by their names – the exception was the Associated Examinating Board (AEB) created to offer ‘O’ and ‘A’ levels to technical colleges. The timing of the A levels examinations and subsequent publication of the results was determined by the beginning of the university year and indeed this led to the way schools and colleges then set their teaching year. Critics have long argued about the lack of flexibility in the ‘scholastic year’ and this has caused innumerable problems for organisations wishing to release people to study at educational institutions at times that suited them. Interesting to reflect on the problems faced by college management when extended year programmes and multiple starting dates were required by the Manpower Services Commission (MSC). Staff were hostile to possible changes in their conditions of service and college management had to employ more part-timers and develop other staff deployment tactics in order to cover the programme schedules. The teachers of the vocational courses accepted the extended year more readily and were conscious of the needs of the employers and funding agencies. These problems were more manifest in general FE colleges which offered a wide range of vocational, professional programmes as well as ‘A’ levels. This aspect also caused tensions between the staff teaching across these different courses as inevitably there were mismatches in the teaching years and very often college managers would receive deputations from vocational staff about the inequalities that this created.
 The pervasive influence of ‘A’ levels has affected negatively the way post-16 education and training has been managed and operated over many years. I am very aware many staff and managers in the education system will disagree with me but having seen at first hand these various consequences I look forward to a government of the day carrying out a radical and fundamental root and branch reform of the examination system post-16 which removes the vocational academic divide and establishes parity of esteem between vocational, work based and academic qualifications. Only then can we truly address the current problems associated with skills shortages and better prepare students to enter employment and university to studysuch subjects as science, mathematics, statistics, engineering, modern languages etc. – with a post-16 qualifications, curriculum and examination system that realises breadth, balance and depth. Then and only then will we begin to increase our international competitiveness and compete in the global market. The current government’s thinking about the development of vocational diplomas is yet another example of the paucity of understanding from politicians It will be interesting to see if the current administration (2010 +) tackle the issue of ‘A’ levels and the reform of the examination system particularly with another attempt to introduce vocational qualifications – I am not optimistic!
Final observation about GCE ‘A’ Levels by providing  a simple comparison between them and equivalent qualifications in Europe aimed at the same age group. This comparison highlights the narrowness, selectivity and rigidity of ‘A’ levels. These characteristics make it difficult to introduce any real change in the structure – what changes have occurred have been incremental and slight. A root and branch reform would be impossible – basically they need to be completely removed from the examination system. But the current government, as with previous ones, are reluctant to carry out any fundament reform let alone remove them from the qualifications framework – the public schools and middle England would vigorously resist that!

GCE ‘A’ levels curriculum

Other similar European curriculum (amalgam of the various countries approaches)

Small number of subjects typically four or less studied in depth

More subjects typically five or more studied in less depth

Free choice of subjects by students

Less student choice constrained by compulsory core subjects

No criteria for an overall curriculum

Overall criteria given what constituents a curriculum

Emphasis on end of course external examination

A variety of assessment approaches e.g. teacher assessment, written exams etc.

No relationship between subjects

Some subjects require a theory of knowledge element

Schools and colleges responsible for the whole curriculum

Examination requirements and national regulations determine and define the whole curriculum

No automatic right to enter Higher Education –admission depends on grades

Automatic right (legal) to enter university in most countries if examination is passed

Reliability of results dependent on the independence of examination boards

Reliability dependent on state examinations or trust in teachers e.g. Germany and Sweden

Examinations can be a mix of linear and modular syllabuses

Modular syllabuses non-existent
Source: Hodgson. A and Spours. K. ‘Dearing and Beyond.’  ISBN 0 7494 2160 6. Kogan Paul. `1997.

Is Mathematics Fit for Employment?

Posted by & filed under Articles.

 The answer to this long standing question is a resounding no! This is especially certainly true for the mathematics that will be required by most post-16 learners who will progress into employment. The subject is most certainly, fundamental and essential as a body of knowledge but it is the way it is taught and learnt that precipitates the problems. This is particularly important in its application in the workplace and the ability of people to use basic mathematical concepts in everyday life. The level of understanding and ability of the majority of people to apply mathematical and numerical concepts is woefully inadequate in England to cope with the future challenges whether in employment or life in the increasingly scientific and technological world. This sad state is not new one only has to review the innumerable reports, commissions, working parties, focus groups and supposed think traps over the decades. Many of these have presented excellent surveys of the situation but with little effect or impact either in the short and long term. Think tanks indeed! What is needed is DO tanks in the long term! This country is world class in creating bodies to address important issues but these are seldom capable of developing effective and sustained strategies and tactics that bring about solutions to this incredibly important problem.

The evidence from these reports is a matter of record accumulated over many decades and have consistently highlighted the inevitable crisis’s that will confront this strategically important subject at all levels where it is required. Problems exist at all sectors of education, training, in the workplace and with functional numeracy.
Many causes and effects have contributed to this sad state of affairs and include:
  • Cultural factors
  • The existing qualifications frameworks for mathematics and numeracy are flawed and require root and branch reform NOT fudge and mudge/tinkering approaches
  • The way mathematics and numeracy programmes are taught and learnt and this coupled with poor teaching produced a damaging cocktail
  • The environment in which teaching and learning takes place – this is particularly relevant for technical and vocational education and training – the context is absolutely critical for successful and sustained learning
  • The obsession with assessment and testing regimes e.g. teaching to the test syndrome – this results in distortion of content and learning and leads to a lack of understanding of the subjects
  • Issues associated with whether or not learning mathematics is perceived as either a pleasurable or painful experience by many learners. (the Cockcroft Report (1982) highlighted this factor)
  • The general perception of mathematics, particularly by peers, parents and society in general towards the subject
  • The lack of perceived obviousness or immediacy so that people do not turn to mathematics as a first resort to solve everyday problems or to understand the world.
  • People often claim to survive and earn a living without having to resort to mathematics
  • The increased use of computers, calculators and ICT multimedia with little thought of how these techniques and technologies are managed to develop critical capability. Badly managed teaching and learning methods using these techniques creates a passivity or acceptance in the way people want to or indeed expect to learn. A number of commentators have suggested that the obsession of retrieving information from the internet without the critical second stage of reflection, analysis and verification will eventually bring about an outsourcing of the memory to the internet. A thought – could these technologies actually erode the crucial element of curiosity so essential in the learning and understanding of these subjects?
  • Many textbooks are still narrow or mechanical in format and content. Teachers and learners must have access to a wide range of learning materials which are fit for purpose for the learner’s ability and future needs whether for further, higher education and ultimate employment. It is essential that the learning resources are managed effectively by the teachers and this requires appropriate initial and CPD programmes
Perhaps it is too simplistic just to view the negative perception towards the subject in terms of a series of causes and effects. If the problem is about the formation of negative attitudes towards the subject then this must be recognised as a complex process that invariably involves the interaction of a number of factors that ultimately cannot be simply or completely identified and explained. Too often commentators are inclined to regard a consequence as a result of a direct relationship between cause and effect. However, this may be an over simplification. As a consequence it might be more productive to think in terms of what factors the problem is related to instead of what causes the problem. In other words it is about the subtle and complex interactions that occur between the contributing facts cited above rather than a simple causation. Any further reviews must attempt to adopt this approach.
Time and space does not allow these elements to be more fully explored in this brief paper as many have been rehearsed  over years but I would like to focus on the critical area of the mathematics and numerical elements required in technical and commercial education and training. Of all the areas of the mathematics problem this is the one that has been the most neglected and ignored. The majority of the reviews have been associated with the so called academic routes i.e. GCSEs, ‘A’ levels and honours degrees with little or no real analysis of the qualifications frameworks for the vast majority of people who require mathematical and numerical skills for the workplace or life in general. I include in this functional numeracy, financial literacy and the needs of people employed in the main occupational sectors of technical and commercial enterprises. This fact mirrors the neglect of technical education and training in this country over centuries .Part of the problem is the hostility and negative view of technical and vocational subjects which are all too often seen as second class. One of the contributing factors to this negative perception and the hostility to technical subjects is that they often include mathematics and if people have an inadequate background or negative experiences of mathematics when entering post-16 studies they will avoid these subjects.
The current qualifications system is skewed towards the supposed needs of academic study with the misplaced assumption that the content is relevant for all those who will progress onto enter most employment. Any effective curriculum framework must possess the essential characteristics of balance, breadth and balance that are fit for purpose for the learner’s employment intentions and needs. The mathematics for employment in addition to possessing the correct balance of these critical characteristics must be seen as relevant both to the learner and also be appropriate to the area of employment that they will enter. Employers must be involved in the development of the programmes not in a tokenistic way but as equal partners in the process. Too often academics state that employers do not know what they require – a classic example of academic elitistism and arrogance! A successful work based education and training system must be predicated and based on an equal working partnership with employers! The evolving apprentice programmes must work closely with employers and their professional bodies in order to create relevant and up-to-date programmes. Awarding bodies particularly those associated with technical, commercial and vocational qualifications must also keep their programmes under constant review and also involve all interested parties through advisory committees especially employers to achieve an effective monitoring function. A number of Further Education colleges have developed innovative and effective ways of teaching the technical and practical but too often resource constraints have curtailed many of these approaches. Some colleges have developed realistic working environments (RWEs) and as a result are more able to provide more relevant context for the learners. Rigid and inflexible curriculum frameworks taught in inappropriate environments too often stifle creative teaching and learning methods.
The way forward.
  • A root and branch review is urgently required of mathematics and numeracy that is truly fundamental and recognises the differences that are required in content, emphasis, relevance and ultimate use of the subject by the whole spectrum of learners.
  • Many of the problems start at primary school and the reviews must once and for all identify meaningful actions that build a strong foundation for the subject for progression on to the secondary stage of education. A good start has been made with the Rose and Williams report but much, more needs to be done.
  • GCSEs and ‘A’ levels are a mess and urgently need a significant over haul -they are most certainly not fit for purpose for the majority of learners.
  • Pre-16 learners who intend to undertake apprenticeships or enter college to study technical and commercial programmes must have opportunities and access to more relevant and appropriate work related experiences. Previous attempts such as application of number, functional mathematics have had a limited impact and a radical rethink is urgently required. Attractive and appropriate learning environments must be created in order to facilitate more and or more effective partnerships with local colleges and employers established.  
  • Post- 16 education and training also requires an urgent review particularly if the school leaving age is raised – the situation will become even more fractured with leaner’s if they have to do more of the same! A comprehensive new set of qualifications are urgently required that are fit for purpose for all the learners.
  • Existing technical and vocational programmes must be made more flexible and teachers given more freedom to innovate work based education and training methods. Colleges must be resourced more adequately. The creation of more realistic working environments (RWEs) is essential to establish the correct context for teaching and learning. In addition enhancing links with employers by increasing work placements/sandwich programmes for learners with the relevant employers in order to show how mathematics and numerical concepts are used in the work place.
  • The major technical and vocational awarding bodies should as a matter of urgency carry out a fundamental review and audit of their mathematical content of all its programmes to see if they match the requirements of the occupational sectors that the programmes are aimed at.
  • The major technical and vocational awarding bodies should establish stronger working links with mathematics organisations and bodies and establish more effective lobbying strategies to government, politicians and civil servants.
 
 

The Importance of Context

Posted by & filed under Articles.

Context – Associated surroundings and settings
               – The circumstances relevant to something under consideration
               – Its true meaning
Functionality –The capacity to be practical and functional
                        – Specific application
The current focus on the vocational curriculum has resulted in the development and possible introduction of the so-called vocational diplomas, a revised programme for apprenticeships and the concept of functionality in such subjects in mathematics and literacy. In addition the proposed raising of the school leaving age has rekindled the age-old debates on how to make such programmes attractive and relevant to learners.
A number of real challenges exist when addressing the development of a vocational focus into curricula particularly the content of the material and the critical aspects of ‘how’ and ‘why’ it is taught and learnt. The most critical element in these debates is the context in which subjects are taught and learnt. It is essential that the teaching, learning methods and the environments in which vocational and practical topics are set are appropriate and seen by the learners as being relevant to their course of study and future employment intentions and aspirations.
Previous attempts to introduce and recognise the importance of vocational programmes have largely failed and the current flurry of activity seems yet again to ignore the lessons that should have been learnt from these earlier initiatives. A great deal of effort, money and time has been expended over the past few decades attempting to create a parity of esteem between academic and vocational qualifications. Various initiatives such as General National vocational Qualifications (GNVQs), the Technical Vocational Education Initiative (TVEI), basic skills programmes e.g. application of number, along with numerous initiatives were introduced by the MSC, DfEE and DfES (see the history of technical education for more details of these initiatives). All failed because of a complex mix of factors such as the negative perception, of both learners and society, of the value of technical education and training resulting in the subsequent second class status of employment in trade, craft and technician occupations. The so-called academic route i.e. GCE and GCSE has always been perceived as superior and attempts to establish parity of esteem between the academic and vocational routes have successively failed. Government interference and ignorance have not helped in these endeavours.
One long standing factor associated with these developments is the damaging and sterile arguments by many of the specifications writers, who are usually pure mathematicians, who have stated that ‘the context makes no difference to the learning and teaching process and that it can be distracting from the real mathematics’. So does this mean that mathematics taught in a practical environment is non-real? How can appropriate teaching and learning environments be created for locating mathematical subjects in the relevant vocational context? Two distinct but related aspects need to be recognised and carefully configured, comprising the basic topics and the application of those topics into a particular vocational setting.   Firstly all learners need to be competent and confident in the basic elements of number and certain key mathematical topics and operations such as arithmetic, algebra etc that form the fundamental building blocks. The second aspect is the application of these basic elements as required in particular employment areas. The first challenge is to make the connection between these two essential aspects particularly the relevance for the learner namely the value and relevance of the basic operations and their subsequent application in an employment context/setting.
The next complication is the wide diversity of the mathematical requirements across the multitude of employment areas. The limited research of mathematics in the work place has identified and highlights this challenge. Essential topics identified include conversions involving %/ fractions/imperial and SI units, transpositions, estimation, the need to understand the importance of tolerances/errors etc. Many teachers and tutors in FE have for decades succeeded in getting students to understand and adapt mathematical operations to their work environments. Many of these teachers have worked in those employment areas or are part-time tutors still active in the relevant industry or service and as a result fully appreciate what is required. Having taught a wide range of CGLI, ONC/OND and HNC/HND programmes in such courses as hairdressing, construction studies, institute of meat, medical laboratory technician’s one quickly understands the challenges. Imagine the challenge of explaining the importance of ph values to hairdressing students! These challenges can be addressed but only if the teacher/tutor fully understands and appreciates how the basic mathematics is to be applied. They have to have direct experience of the applications and teach those elements in the appropriate environment/setting. Much can be achieved through simulation or more effectively in a real work environment (RWE). This approach immediately presents problems for the institution and the teacher, particularly resources e.g. financial, human and physical. Teachers must be qualified and experienced; institutions must possess the appropriate teaching and learning environments and adequate funding must be available to resource the work. In other words the resources and infrastructure most be fit for purpose.
Some of the best current work in Britain is in the armed forces, particularly in the basic skills of information technology, numeracy and literacy. The entry level of many recruits is very low and the army in particular is achieving excellent results. The need for the modern army to be proficient in application of number and IT requires personnel to understand complex mathematical concepts in such areas as navigation, weapon techniques and logistics. They also need to be able to communicate, with people in countries where they are active, in English and elements of foreign languages when posted abroad. The Services most certainly exploit real working environments and the results are remarkable. Obviously the situations are not so demanding or extreme for other professions but the armed forces highlight the advantages of teaching and learning in real contexts.
Space only allows one example of how tutors have attempted to create the correct teaching and learning environment. For example in a painting and decorating class the students were introduced to the need to estimate the amount of material to be used to decorate a room. The tutor – a practicing professional – stressed the importance of getting the estimations right as their employer would not appreciate an under or over estimation which would alienate the customer, damage his/her reputation and the profit margin. Under careful guidance in a real working environment the students very quickly understood the importance of estimating quantities of the materials to be used i.e. wall paper, paints, the correct sizes of brushes etc. They began to easily and confidently quantify areas, paint volumes and tolerations/errors, conversion of imperial/SI units and costings. Yet before the course they would openly deny that they understood mathematics and that they hated the subject.
In order for the current development of vocational programmes and functional mathematics to be successful a great more attention needs to be given to context.

Finsbury Technical College (1883-1924) and the Central Institution

Posted by & filed under Biographies & Pen Portraits.

One of the aims following the creation of the City and Guilds of London Institute in 1878 was to establish a Central Institution in London to improve the training of craftspeople. The CGLI was initially unable to find premises of a suitable size for the Central Institute and as a result founded the Finsbury Technical College, which would act as the first feeder for the Central Institution. The college opened in 1883 and is now recognised as the first technical college in England. Its design was to be ‘model trade school for the instruction of artisans and other persons preparing for intermediate posts in industrial works’. The college was formed out of the Cowper Street Schools where some evening classes were already being offered before the City and Guilds Institute assumed responsibility in 1878. Philip Magnus had taught mechanics at the Cowper Street site before he gained the position at the CGLI. The college offered opportunities for daytime and evening study and subjects included building, design, drawing, engineering, mathematics and science. Philip Magnus the first secretary and organising director and was ably supported by a number of remarkable professors who between them quickly established the college as a centre of innovative and progressive instruction. As a result the Finsbury Technical College quickly established its credibility as a successful institution and this subsequently provided the future model for the pattern of technical colleges across the country. Its success depended greatly on the founding professors namely Henry Armstrong (1848-1937), William Ayrton (1847-1908), Silvanus Thompson (1851-1916) and John Perry (1850-1920). Armstrong for example was able to develop and refine his revolutionary methods of teaching science at the college. Silvanus P. Thompson was professor of physics and later was Principal of the Finsbury College for thirty years. William. E. Ayrton (1847-1908) was Professor of Physics and Telegraphy (1883-1884) and went on to become a Professor at the Central Institution (1884-1908) when that was finally created in 1884. John Perry was a brilliant electrical engineer who had been Kelvin’s assistant at Glasgow and also worked with William Ayrton at the Imperial College of Engineering in Tokyo (see biography of these remarkable individuals on this website).
The Central Institution was eventually opened in 1884 in a purpose designed building in South Kensington adjacent to the Royal School of Mines (RSM) and the Royal College of Science (RCS). In 1907 the RSM and the RCS were incorporated into Imperial College and the Central Institution was renamed the City and Guilds College and subsequently incorporated into Imperial College in 1910 and became an established and noted engineering college. A picture of the Central Institution is shown below.
Central Institution
  
 References:
‘The Journal Nature’.  Page 807. 24th November 1936.

Sir Philip Magnus (1842-1933)

Posted by & filed under Biographies & Pen Portraits.

Educationalist, First Secretary of the CGLI and Founding Principal of Finsbury Technical College.
Born in London Philip Magnus studied at University College, London graduating in the Arts in 1863 and the University of London graduating in science in 1864. After graduating he continued his theological studies between 1865 and 1866 in Berlin. On returning to London he became a minister at the Berkeley Street Synagogue but gradually became more involved in teaching, lecturing and examining. Philip Magnus in addition to his private teaching he was professor of the Catholic University and wrote a text book entitled “Lessons in Elementary Mechanics” that became a standard work for many years. He increasingly questioned the existing practices and systems of education and was perceived as a radical.
Soon after the City and Guilds Institute of London for the Advancement of Technical Education (CGLI) assumed responsibility for the technological examinations from the Society of Arts (SoA/[R]SA) an  advert appeared in Nature for the position of an “Organising Director and Secretary”. The post initially was part-time and carried an annual salary of £ 400. Philip Magnus was the successful candidate who because of his background and being a person possessing the necessary vision to develop new and innovative approaches to technical education was seen as an ideal candidate for the position. One of the first challenges was to manage the very successful Technical School in Cowper Street, London. The student numbers had grown significantly and the existing accommodation and facilities were now inadequate. An extensive range of evening classes were provided for artisans wanting to learn about the basic principles of they work. Classes were provided for chemists, dentists, engineers, telegraphics, and printers – the list was truly remarkable. Eventually on 26th July 1880 the CGLI Executive Committee agreed to establish a new institution namely the Finsbury Technical College. Philip Magnus was appointed as its first Principal (1883-1885) and drafted the overall strategy for the new institution. The task of developing the schemes of work and methods of instruction fell to the professors namely Henry Armstrong (1848-1937) (1), William Ayrton (1847-1904) and Silvanus Thompson (1851-1916). Thompson later became Principal of the College and held the post for thirty years. These three remarkable individuals pioneered new teaching techniques in science education particularly the experimental aspects of science and electricity. [I  have provided more detail about the Finsbury College and its teachers in a separate biography]. Magnus was the driving force behind the development of the college. Even at this time he was highlighting through his writings and lectures the massive investment in technical education being made in Germany compared with Britain and the consequences for Britain’s industrial future. He wrote a seminal text book on Mechanics and his publication “Industrial Education” (1888) is considered a classic of its kind. He was very influential in the development of the Central Institution located in South Kensington, (opened in June 1884), and its existence was due to the support from the City and Guilds both financially and through the expertise of Magnus. Magnus was a member of the London School Board in 1890 and 1891, a fellow of the London University Senate from 1900 and Chairman of the Education Committee of the Borough Polytechnic. Sir Philip Magnus became the leading authority on technical education and was a significant and influential member of the Royal Commission on Technical Instruction – the Samuelson Report (1881–1884). 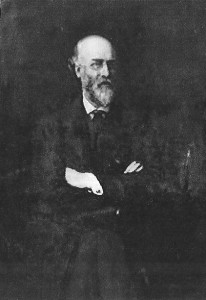Portrait of Bernard Samuelson shown below.
Bernard Samuelson
In spite of his status and reputation he experienced many setbacks during his life and career for further details see Lang (2). A remarkable individual and a great supporter of the creation of technical education who made significant contributions to its development.
 Magnus wrote two excellent books: Educational Aims and Efforts 1880-1910′ Longmans, Green, and Co. 1910. and ‘Industrial Education’ Kegan Paul, Trench and Co. 1888. London – well worth reading.
(1)   Van Preach. G. ‘H.E. Armstrong and Science Education.’ John Murray. 1973.
(2)   J. Lang. “City and Guilds of London Institute. Centenary 1878 – 1978.” CGLI publications. 1978.
(3)   B. Bailey. “Sir Philip Magnus.” Oxford Dictionary of National Biography. 2004.
(4)   F. Foden. “Philip Magnus: Victorian Educational Pioneer.” Vallentine, Mitchell-London. 1970. Frank Foden has written the seminal biography of Magnus.
(5)   P. Magnus. “Industrial Education.” K. Paul and French and Co. 1888.

Bernhard Samuelson (1820-1905)

Posted by & filed under Biographies & Pen Portraits.

Educationalist, Industrialist, Liberal Politician and Pioneer of Technical Education
 
Born in Hamburg and brought up in Hull and educated at the Rev J Blezard’s school he started work in his father’s business and was then apprenticed to a Swiss company in Liverpool. After the apprenticeship he worked in a manufacturing firm Sharp, Stewart and Company based in Manchester that exported machinery. This appointment gave him opportunities to travel extensively across Europe. Samuelson was now a qualified iron-master and gained extensive experience of exporting locomotives and machinery. Samuelson bought a small agricultural manufacturing company in Banbury in1848 and made a great success of this enterprise helping to turn Banbury from a market town into a major industrial centre and by 1872 was producing 8,000 reaping machines. Also the production of iron, tar and other products from his ironworks had grown significantly.  As a result he became a very successful businessman with factories in America, France and was instrumental in developing the iron and steel complex on Tees-side and at Newport. He became active in politics from 1865 until 1895 serving in the Gladstone administrations and as an MP represented Banbury and later North Oxfordshire. Samuelson had a wide range of interests ranging across such subjects as: industrial issues, mathematics, modern languages, music and the urgent need to develop technical education. He became well known for his advocacy of scientific and technical education. Not unsurprisingly Samuelson was not a typical businessman particularly at this time being passionate about the diffusion/spread of scientific and technical knowledge and concepts whilst managing major business enterprises and holding down a political career.
From 1867 he travelled widely and made a detailed comparative study of European technical education drawing insightful conclusions about the English education system particularly technical education. As a result of his interests he wrote many technical papers and chaired committees on these subjects. Samuelson chaired the first formally established parliamentary investigation into education and industry in 1868 and was appointed chair to the Royal Commission on Technical Education (1882-84). In addition he served on the Devonshire Commission representing the Science and Art Section of the Report. He also was a member of the Cross Commission (1888). He was elected an FRS in 1881. In 1884 Samuelson, see portrait opposite, created a technical institute in Banbury that was formally opened by Antony Mundella (1825-1897).
He was a member of the the Institution of Civil Engineers, a member of the Institution of Mechanical Engineers and an FRS.
Samuelson in the preface to ‘Technical Education’ (1) (F.C. Montague 1887) voiced concern about the inadequate level of funding for scientific studies and that technical institutions were in constant financial difficulty being ‘inadequately provided with funds and not numerously frequented’. Throughout his life he was a strong advocate for the creation of high standards of technical education in Britain that were comparable to those he had witnessed in his travels in Europe.
Useful references:
(1)   Montaque. F. C. ‘Technical Education.’ Cassell. 1887.
       and the Oxford Directory of National Biographies.